Quantum permutations represent a groundbreaking intersection of quantum mechanics and combinatorial theory‚ offering novel approaches to problem-solving and computational advancements.
Understanding the Basics of Quantum Permutations
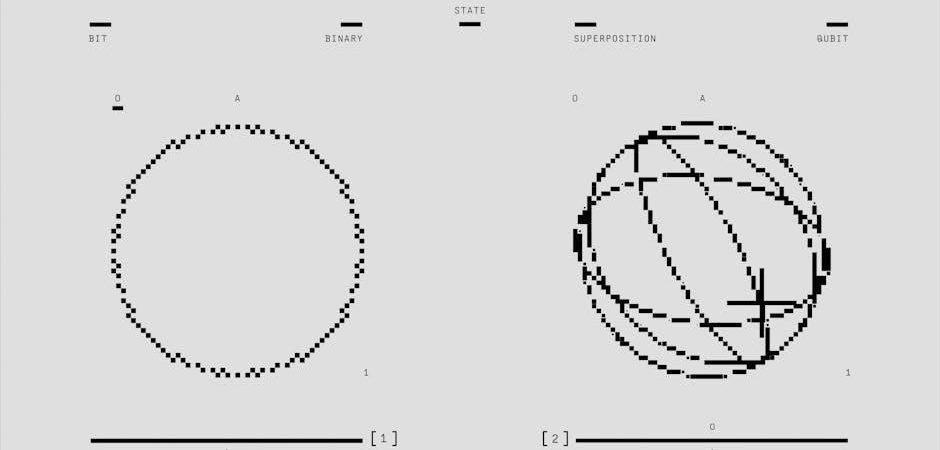
Quantum permutations introduce a new paradigm by extending classical permutations into the quantum realm. Unlike classical permutations‚ which rely on fixed‚ deterministic arrangements‚ quantum permutations leverage the principles of quantum mechanics. These include superposition‚ where a quantum system can exist in multiple states simultaneously‚ and entanglement‚ enabling correlations between qubits. By representing permutations as quantum states‚ quantum permutations allow for the exploration of exponentially larger solution spaces. This property makes them particularly promising for solving complex combinatorial problems. The foundation of quantum permutations lies in the interplay between quantum bits (qubits) and their unique abilities to process information in parallel. This duality between classical and quantum perspectives opens new avenues for computational advancements‚ blending the discrete nature of permutations with the continuous possibilities of quantum mechanics. Understanding these basics is crucial for harnessing their potential in various fields‚ from optimization to machine learning.

What Are Quantum Permutations?
Quantum permutations extend classical permutations into the quantum realm‚ utilizing qubits to enable simultaneous processing of multiple states‚ revolutionizing combinatorial problem-solving.
Definition and Scope of Quantum Permutations
Quantum permutations involve applying quantum principles to combinatorial arrangements‚ enabling superposition and entanglement of states. Unlike classical permutations‚ which are fixed sequences‚ quantum permutations allow for the simultaneous existence of multiple arrangements. This concept leverages qubits to process various configurations probabilistically‚ enhancing computational efficiency. The scope encompasses theoretical frameworks‚ algorithmic implementations‚ and practical applications in fields like cryptography and optimization. Researchers explore how quantum mechanics can solve complex permutation problems more efficiently than classical methods‚ though challenges like quantum noise and scalability must be addressed to realize their potential fully.
The Role of Quantum Mechanics in Permutations
Quantum mechanics introduces revolutionary principles to permutations‚ such as superposition‚ entanglement‚ and interference. These phenomena enable quantum systems to explore multiple permutation states simultaneously‚ unlike classical systems‚ which process one permutation at a time. By leveraging qubits‚ quantum mechanics allows for the parallel evaluation of vast combinatorial spaces‚ significantly accelerating certain computational tasks. The probabilistic nature of quantum states also provides unique insights into solving complex permutation-based problems. This integration of quantum principles opens new avenues for efficient algorithms and enhances our understanding of combinatorial optimization. The interplay between quantum mechanics and permutations is a cornerstone of quantum computing’s potential to revolutionize computational problem-solving.

Importance of Quantum Permutations
Quantum permutations offer transformative computational capabilities‚ enabling efficient solutions to complex problems and unlocking new possibilities in quantum computing‚ optimization‚ and beyond.
Applications in Quantum Computing
Quantum permutations provide a novel framework for quantum computing‚ enabling the manipulation of qubit states in ways that classical systems cannot. By leveraging superposition and entanglement‚ quantum permutations allow for parallel processing of multiple states simultaneously‚ significantly speeding up certain computations. This capability is particularly valuable in algorithms like Shor’s and Grover’s‚ where permutations play a crucial role in achieving quantum speedup. Additionally‚ quantum permutations facilitate the exploration of vast solution spaces in optimization problems‚ making them indispensable for tackling complex tasks. Their role in quantum error correction further enhances the reliability of quantum systems‚ ensuring robustness against decoherence and noise. Overall‚ quantum permutations are essential for advancing quantum computing‚ offering unparalleled efficiency and innovation in computational processes.
Impact on Cryptography and Security
Quantum permutations revolutionize cryptography by introducing quantum-enhanced security protocols and challenging classical encryption methods. Quantum computing’s ability to process permutations exponentially faster threatens traditional cryptographic systems‚ such as RSA and ECC‚ which rely on factorization and discrete logarithms. This necessitates the development of quantum-resistant algorithms. Concurrently‚ quantum permutations enable secure communication through quantum key distribution‚ leveraging entanglement for unconditional security. They also enhance cryptographic protocols by generating unbreakable encryption keys and enabling secure multi-party computation. As quantum systems scale‚ they promise to transform cryptography‚ offering both threats to legacy systems and innovative solutions for secure communication in the quantum era.

Key Concepts in Quantum Permutation Instructions
Key concepts in quantum permutation instructions include qubits‚ superposition‚ entanglement‚ and quantum gates‚ forming the foundation for quantum operations and enabling advanced computational tasks.
Quantum Bits and Qubits
Quantum bits‚ or qubits‚ are the fundamental units of quantum information‚ differing from classical bits by their ability to exist in superposition and entanglement. Unlike classical bits‚ which are either 0 or 1‚ qubits can simultaneously represent both states‚ enabling parallel processing. Qubits are typically realized through quantum systems like electrons‚ photons‚ or superconducting circuits‚ where their state is described by a complex probability amplitude. This unique property allows qubits to perform computations exponentially faster than classical bits in certain tasks. Entanglement‚ a phenomenon where qubits’ states are correlated regardless of distance‚ further enhances computational power; Understanding qubits is essential for grasping quantum permutation instructions and their applications in quantum computing.
Superposition and Entanglement
Superposition and entanglement are fundamental quantum phenomena that enable quantum computers to process information in ways classical computers cannot. Superposition allows qubits to exist in multiple states simultaneously‚ enabling parallel processing. Entanglement links qubits so the state of one instantly influences another‚ regardless of distance. Together‚ these phenomena allow quantum computers to perform complex tasks‚ like certain permutations‚ more efficiently. Superposition enables exploring multiple possibilities at once‚ while entanglement maintains correlations between qubits. These principles are crucial for quantum permutation instructions‚ offering potential breakthroughs in cryptography‚ optimization‚ and more. However‚ challenges like maintaining coherence and scalability must be addressed to fully harness their power.
Quantum Gates and Operations
Quantum gates and operations are the building blocks of quantum computing‚ enabling the manipulation of qubits to perform complex computations. These gates‚ such as Hadamard‚ CNOT‚ and SWAP‚ implement specific transformations on qubit states. They are essential for creating quantum circuits that process information in ways classical systems cannot. Quantum gates leverage superposition and entanglement to execute operations like quantum parallelism. Permutation instructions rely on these gates to rearrange qubits and their states‚ facilitating tasks such as quantum Fourier transforms and simulations. The precision and scalability of quantum gates are critical for achieving practical quantum advantage. However‚ challenges like gate errors and noise must be addressed to ensure reliable operation in large-scale quantum systems.

How Quantum Permutation Instructions Work
Quantum permutation instructions manipulate qubits through controlled operations‚ enabling the rearrangement of quantum states to achieve specific computational tasks while maintaining quantum coherence.
The Mathematics Behind Quantum Permutations
Quantum permutations are rooted in group theory and linear algebra‚ where permutations are represented as unitary matrices acting on Hilbert spaces. These operations preserve quantum states’ integrity‚ enabling precise state transformations. The mathematical framework involves tensor products and probabilistic interpretations‚ ensuring coherence and superposition principles are maintained. Quantum algorithms leverage these properties to solve permutation-based problems efficiently‚ often outperforming classical counterparts. The interplay of algebraic structures and quantum mechanics forms the backbone of permutation operations‚ making them indispensable in quantum computing and information theory. Advanced mathematical tools‚ such as representation theory‚ further enhance the analysis and implementation of quantum permutation instructions.
Algorithmic Implementation of Permutations
Implementing quantum permutations involves translating classical permutation algorithms into quantum circuits‚ leveraging quantum phenomena like superposition and entanglement. Quantum algorithms‚ such as those using the Quantum Fourier Transform‚ are designed to efficiently manipulate quantum states and perform permutations. These algorithms are structured to minimize quantum noise and maximize coherence‚ ensuring reliable operation. The process often involves breaking down permutations into elementary quantum gates‚ which are then executed sequentially. Challenges arise in maintaining quantum states’ stability and correcting errors‚ but advancements in quantum error correction have improved robustness. This approach enables quantum systems to solve permutation-based problems with unprecedented efficiency‚ offering significant advantages over classical methods in certain scenarios.

Applications of Quantum Permutation Instructions
Quantum permutation instructions enable advanced solutions in cryptography‚ optimization‚ and machine learning‚ enhancing security‚ efficiency‚ and data processing capabilities across diverse computational domains.
Optimization Problems and Quantum Permutations
Quantum permutations offer revolutionary approaches to solving complex optimization problems by leveraging quantum parallelism and interference. These phenomena allow quantum systems to explore vast solution spaces simultaneously‚ significantly speeding up the identification of optimal permutations. Traditional optimization challenges‚ such as logistics‚ scheduling‚ and resource allocation‚ can benefit from this quantum advantage. Quantum algorithms‚ like the Quantum Approximate Optimization Algorithm (QAOA)‚ are being developed to tackle permutation-based problems more efficiently than classical methods. This capability has profound implications for industries relying on optimization‚ enabling faster and more accurate decision-making. As quantum technology advances‚ the integration of quantum permutations into optimization frameworks promises to unlock new levels of computational efficiency and innovation.
Machine Learning and Quantum Permutations

Quantum permutations are poised to revolutionize machine learning by enabling faster and more efficient processing of complex datasets. By leveraging quantum parallelism‚ these permutations can accelerate tasks like pattern recognition‚ feature selection‚ and clustering. Quantum-enhanced algorithms‚ such as quantum k-means and quantum support vector machines‚ utilize permutation-based operations to improve classification accuracy and reduce computational overhead. Additionally‚ quantum permutations can optimize neural network architectures by exploring multiple configurations simultaneously‚ leading to faster training and better generalization. However‚ integrating quantum mechanics with classical machine learning frameworks presents challenges‚ such as quantum noise and the need for robust error correction. Despite these hurdles‚ the synergy between quantum permutations and machine learning holds vast potential for advancing AI systems and solving previously intractable problems.

Challenges in Implementing Quantum Permutation Instructions
High error rates‚ quantum noise‚ and maintaining precise qubit control are significant challenges‚ along with scalability limitations and algorithmic complexity in quantum permutation implementations.
Quantum Noise and Error Correction
Quantum noise poses a significant challenge in implementing quantum permutation instructions‚ as it introduces errors in qubit states due to environmental interactions. Unlike classical systems‚ quantum errors are continuous and harder to detect. Quantum error correction codes‚ such as surface codes and Shor codes‚ are essential to mitigate these issues. However‚ implementing robust error correction requires redundant qubits and complex encoding schemes‚ increasing hardware demands. Additionally‚ the sensitivity of qubits to noise complicates the scalability of quantum systems. Addressing these challenges is critical for achieving reliable quantum computation‚ as errors propagate quickly in quantum circuits‚ potentially invalidating permutation operations. Ongoing research focuses on developing noise-resilient algorithms and improving error correction techniques to enhance the practicality of quantum permutation instructions.
Scalability Issues in Quantum Systems
Quantum permutation instructions face significant scalability challenges as the number of qubits increases. Maintaining control over a growing number of qubits while minimizing errors becomes complex. Quantum systems require precise alignment of quantum states‚ which is difficult to achieve at scale. Additionally‚ the instability of qubits due to decoherence and noise further complicates large-scale implementations. Current quantum architectures struggle to handle the exponential growth of computational requirements for permutation operations. Technical challenges‚ such as cryogenic cooling for superconducting qubits and photon loss in optical systems‚ add layers of complexity. Scalability is a critical barrier to practical quantum permutation applications‚ requiring breakthroughs in quantum hardware and control mechanisms to overcome these limitations and enable efficient large-scale computation.

Future Directions and Research
Future research in quantum permutation instructions focuses on advancing quantum hardware‚ developing robust quantum algorithms‚ and exploring interdisciplinary applications to unlock new computational possibilities and efficiencies.
Advancements in Quantum Hardware
Advancements in quantum hardware are pivotal for enabling practical quantum permutation instructions. Enhancing qubit stability‚ quantum gate precision‚ and error correction mechanisms are critical challenges. Recent breakthroughs in superconducting qubits and trapped ions have improved coherence times and gate fidelities‚ paving the way for more reliable quantum systems. Scalability remains a significant hurdle‚ with efforts focused on integrating more qubits while maintaining control. Researchers are also exploring hybrid quantum-classical systems to optimize performance. The development of fault-tolerant quantum computers is essential for large-scale implementations of quantum permutation instructions. These hardware improvements will directly impact the efficiency and applicability of quantum permutation-based algorithms across various domains.

Development of New Quantum Algorithms
The development of new quantum algorithms is crucial for fully harnessing the potential of quantum permutation instructions. Researchers are focusing on creating algorithms that leverage quantum parallelism and interference to solve complex combinatorial problems more efficiently than classical methods. These algorithms are being designed to address challenges in optimization‚ cryptography‚ and machine learning‚ where permutations play a central role. Innovations in quantum circuit synthesis and error-mitigation techniques are enabling more robust implementations. Additionally‚ hybrid quantum-classical algorithms are being explored to bridge the gap between current hardware limitations and theoretical capabilities. As these algorithms mature‚ they promise to unlock transformative applications across industries‚ driving innovation in fields like logistics‚ drug discovery‚ and financial modeling.
Quantum permutation instructions pave the way for revolutionary advancements in computing and problem-solving‚ offering unprecedented efficiency and innovation across diverse fields and industries.
Quantum permutation instructions integrate quantum mechanics with combinatorial mathematics‚ enabling efficient solutions to complex problems. They leverage qubits‚ superposition‚ and entanglement to process multiple states simultaneously‚ enhancing computational power. Applications span quantum computing‚ cryptography‚ and optimization‚ addressing challenges like scalability and error correction. These instructions utilize quantum gates and algorithms to achieve tasks beyond classical capabilities‚ offering transformative potential for secure communication and intelligent systems. Despite current limitations‚ ongoing research promises advancements in hardware and algorithms‚ positioning quantum permutations as a cornerstone of future technological innovation.
Final Thoughts on Quantum Permutation Instructions
Quantum permutation instructions hold immense potential to revolutionize computing and problem-solving by harnessing the power of quantum mechanics. Their ability to process multiple states simultaneously offers unparalleled efficiency‚ making them indispensable for complex tasks. As research progresses‚ advancements in hardware and algorithms will likely overcome current limitations‚ unlocking wider applications. The integration of quantum permutations into fields like cryptography and optimization promises enhanced security and decision-making. While challenges remain‚ the transformative potential of these instructions is undeniable. Continued exploration and innovation will be key to unlocking their full capabilities‚ ensuring quantum permutations play a pivotal role in shaping the future of technology and computation.